|
На этапе статистической обработки могут быть поставлены самые различные задачи исследования, для решения которых нужно выбрать соответствующую среднюю. При этом необходимо руководствоваться следующим правилом: величины, которые представляют собой числитель и знаменатель средней, должны быть логически связаны между собой.
Используются две категории средних величин (рис. 2.14):
* степенные средние;
* структурные средние.
Первая категория степенных средних включает: среднюю арифметическую, среднюю гармоническую, среднюю квадратическую, среднюю геометрическую и средняя кубическая.
Рис. 2.14. Виды средних в статистике
Введём следующие условные обозначения:
X- средняя, где черта сверху свидетельствует о том, что имеет место осреднение индивидуальных значений;
Xi- варианты (значение) осредняемого признака или серединное значение интервала, в котором измеряется вариант;
n – число вариант;
f- частота (повторяемость индивидуальных значений признака).
k - показатель степени.
Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными.
Простая средняя считается по не сгруппированным данным и имеет следующий вид:
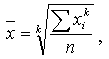 , (2.15)Взвешенная средняя считается по сгруппированным данным и имеет общий вид:
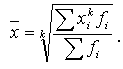 . (2.16)
В зависимости от того, какое значение принимает показатель степени, различают следующие виды степенных средних:
- средняя арифметическая, если k = 1;
- средняя гармоническая, если k = -1;
- средняя геометрическая, если k = 0;
- средняя квадратическая, если k = 2;
- средняя кубическая, если k = 3.
Формулы степенных средних приведены в табл. 2.9.
Таблица 2.9
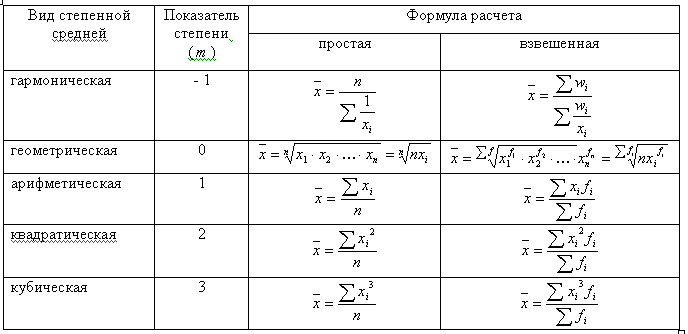
Виды степенных средних
Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени k увеличивается и соответствующая средняя величина:
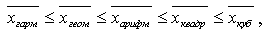 , (2.17) , (2.17)В статистической практике чаще, чем остальные виды средних взвешенных, используется средняя арифметическая и средняя гармоническая взвешенные. Выбор вида степенной средней определяется экономическим содержанием задачи и наличием данных.
Рассмотрим среднюю арифметическую простую и взвешенную.
Пример: Студент Петров по результатам учебного семестра имеет следующие оценки: теория бухгалтерского учета - 4, экономическая статистика - 5, финансы, денежное обращение и кредит - 3, экономика фирмы - 2. Какова его средняя оценка по результатам семестра?
Поскольку каждая оценка встречается один раз, для расчета средней применяем формулу арифметической простой:
Перечисленные дисциплины студент Петров сдал в среднем на 3,5 балла.
Пример: Имеются следующие данные о распределении бригад по уровню выработки продукции (табл. 2.10).
Таблица 2.10
Распределение бригад по уровню выработки продукции за смену
|
Бригады
|
Выработка продукции в среднем на одного человека, шт. (х)
|
Число рабочих, чел. (f)
|
|
1
|
110
|
12
|
|
2
|
120
|
10
|
|
3
|
130
|
14
|
|
4
|
140
|
8
|
|
Итого
|
-
|
44
|
Определим сменную выработку рабочего в среднем по четырём бригадам. Введём строку условных обозначений, приняв за х значения осредняемого признака, f - число рабочих с данным значением х.
Исходные данные представлены в виде дискретного ряда распределения; каждое х встречается несколько раз, следовательно, применяем формулу средней арифметической взвешенной:
В смену рабочий данных четырёх бригад изготавливает в среднем 124 единицы продукции.
Расчёт средней по интервальному ряду
Если исходные данные заданы в виде интервального ряда, то:
1) закрывают открытые интервалы, приняв их равными ближайшим закрытым;
2) за значения осредняемого признака х берут середины интервалов и строят условный дискретный ряд распределения:
где хн.г - значение нижней границы интервала («от»); хв.г - значение верхней границы интервала («до»).
3) расчёт средней производится по средней арифметической взвешенной.
Пример: Имеются данные о распределении рабочих цеха по стажу работы (табл. 2.11):
Таблица 2.11
|
Стаж работы, лет
|
Доля рабочих, % к итогу
|
|
До 5
|
10
|
|
5-10
|
44
|
|
10-15
|
30
|
|
15-20
|
10
|
|
20 и выше
|
6
|
Каков средний стаж работы рабочего данного цеха?
Строим расчётную таблицу, обозначив долю рабочих через f:
|
Стаж работы, лет
|
f
|
х
|
хf
|
|
До 5
|
10
|
2,5
|
25
|
|
5-10
|
44
|
7,5
|
330
|
|
10-15
|
30
|
12,5
|
375
|
|
15-20
|
10
|
17,5
|
175
|
|
20 и выше
|
6
|
22,5
|
135
|
|
Итого
|
100
|
|
1040
|
Закрываем открытый интервал «до 5». Ширина ближайшего закрытого интервала равна 5 годам (5-10), следовательно, наш интервал примет вид от 0 до 5. Аналогично открытый интервал «20 и выше» примет вид 20-25, поскольку ширина ближайшего закрытого (15-20) равна 5.
Находим середину каждого интервала и принимаем ее за значение х.
Исчисляем значения х*f и сумму этих значений, необходимую для расчета средней арифметической взвешенной, заносим результаты в расчетную таблицу.
Определяем средний стаж рабочего:
Рабочий данного цеха отработал в среднем 10,4 года. Расчет средней по интервальному ряду распределения дает приближенный результат за счет того, что за значения х берутся не точные данные, а осредненные значения (середины интервалов).
Средняя гармоническая имеет более сложную конструкцию, чем средняя арифметическая. Её чаще всего применяют для расчётов тогда, когда в качестве весов используются не единицы совокупности – носители признака, а произведения этих единиц на значения признака, т.е. w = xf.
Пример: Имеются данные о реализации продукта одного вида на трёх рынках города:
|
Рынки
|
Цена за ед. продукции, руб. (х)
|
Количество проданной продукции, шт. (f)
|
Выручка от продажи, руб. (w)
|
|
1
|
30
|
100
|
3000
|
|
2
|
35
|
200
|
7000
|
|
3
|
40
|
200
|
8000
|
|
Итого
|
-
|
500
|
18000
|
Следует определить среднюю цену, по которой продавался товар.
При расчёте средней цены на один и тот же товар, который продаётся в трёх разных торговых точках, необходимо выручку от реализации продукции поделить на количество реализованной продукции.
Предположим, что мы располагаем только данными о ценах на трёх рынках и количестве товара, проданного на каждом из них. При этом цены на отдельных рынках выступают в качестве вариантов, а количество проданного товара – в качестве весов. Тогда средняя цена определяется по средней арифметической взвешенной:
Теперь предположим, что количество проданного товара неизвестно, а известны лишь цены и выручка от продажи. В этом случае логические рассуждения остаются теми же, но расчёт следует записать в форме средней гармонической взвешенной:
Результат, как и следовало ожидать, получился тот же.
Пример: допустим, в результате проверки двух партий муки потребителям установлено, что в первой партии муки высшего сорта было 3942кг., что составляет 70,4 % общего веса муки всей партии. Во второй партии муки высшего сорта было 6520кг., что составляет 78,6 % общего веса муки этой партии.
Необходимо определить средний процент муки высшего сорта по первой и второй партиям вместе.
|