Дифференциальное уравнение звена –

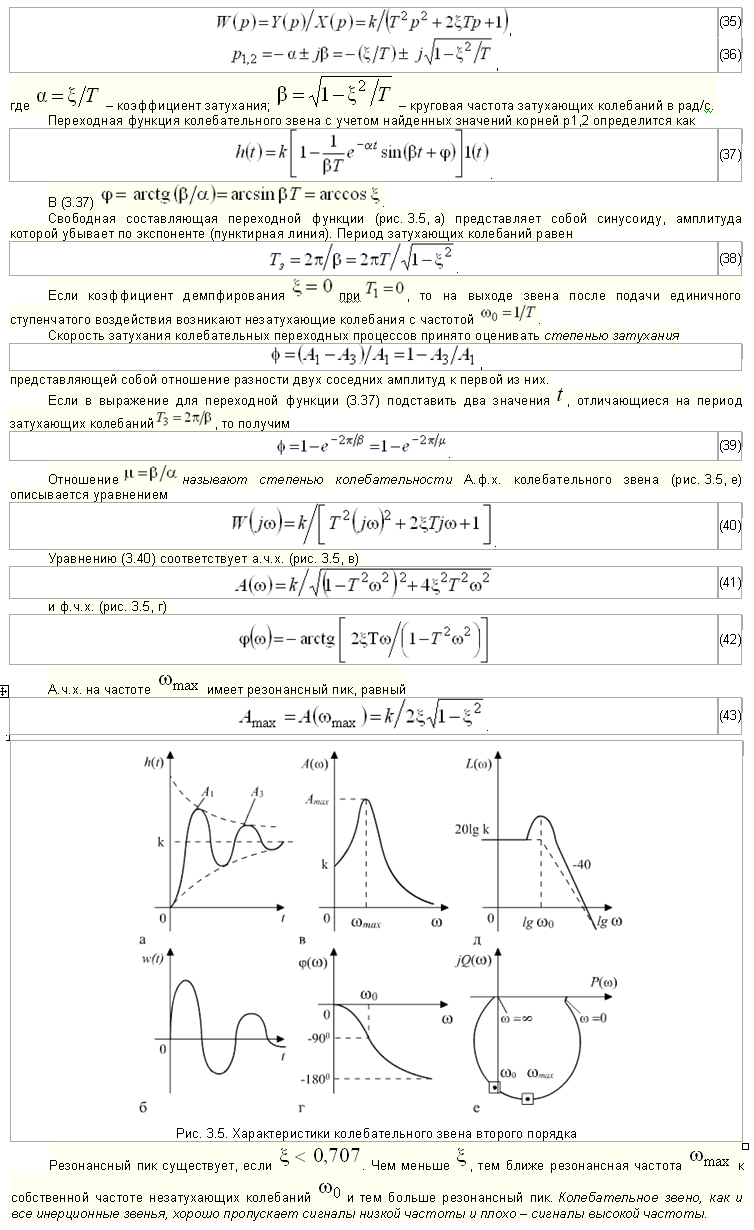
При T1=0 оба корня будут мнимыми, а переходная функция будет представлять собой незатухающую синусоиду. В этом случае звено называют идеальным колебательным или консервативным.

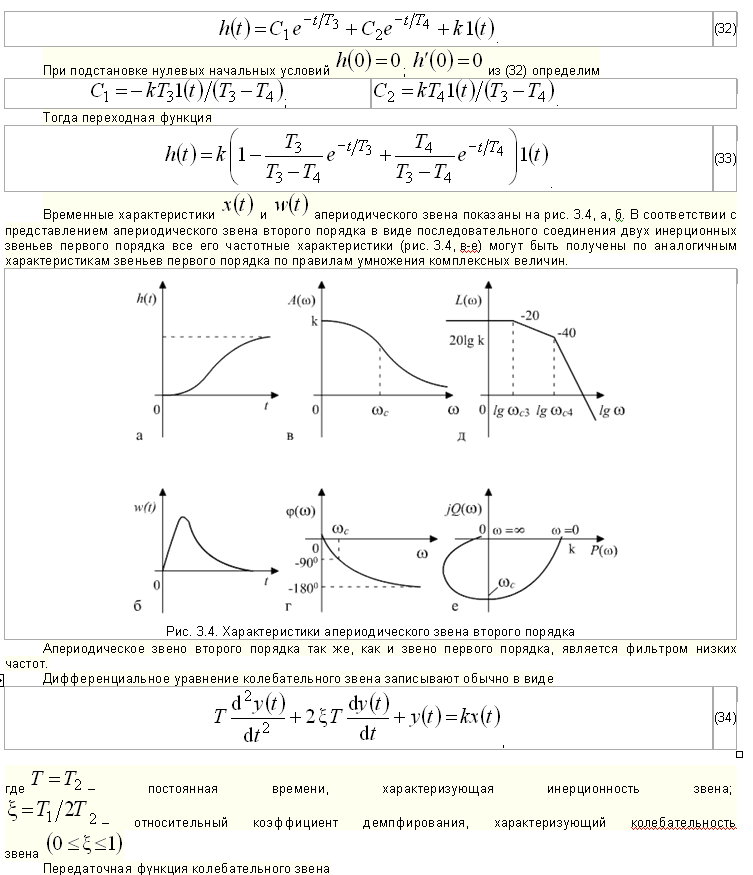
Наряду с общими свойствами (статизм, инерционность) апериодическое и колебательное звенья имеют и существенные различия. Рассмотрим особенности характеристик этих звеньев.

Переходная функция апериодического звена второго порядка может быть получена сложением общего решения (28) с частным решением, соответствующим вынужденной составляющей при x(t)=1(t). Тогда переходная функция определится как