Понятие устойчивости системы регулирования связано с ее способностью возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния.

Понятие устойчивости можно распространить и на случай движения САР:

Устойчивость системы связана с природой самой системы, а не с тем, как внешние источники движущих сил (задание, помехи) заставляют перемещаться ее координаты. Очевидно, что невозможно описать цепь преобразования энергии (систему) не учитывая источников. Поэтому в правой части ДУ описывающих систему всегда будут присутствовать источники движущих сил (вспомните как записываются уравнения по II закону Кирхгофа). Однако если их обнулить, то система ДУ не потеряет смысла. После отключения источников в любой линейной цепи преобразования энергии возникнет переходный процесс обусловленный энергией, которую накопили пассивные реактивные элементы цепи (собственный переходный процесс). Именно он определит, будет ли система устойчивой. И именно эта система ДУ, в которой обнулены величины источников движущих сил, называется характеристической. Если система характеристических ДУ решена относительно одной из координат, то она называется характеристическим уравнением.

Устойчивость систем зависит от корней характеристического уравнения, поскольку его решение есть сумма экспоненциальных функций:

где: A и j - новые постоянные интегрирования, a - показатель затухания, b - круговая частота затухающих колебаний.

Таким образом, для затухания переходного процесса и устойчивости линейной системы необходимо и достаточно, чтобы вещественные части корней были отрицательными, те лежали слева от мнимой оси плоскости корней.

Система будет находиться на границе устойчивости при наличии:

Чтобы корни ХУ имели отрицательные вещественные части, необходимо чтобы все его коэффициенты были положительны. Однако это условие является достаточным только для систем 1-ого и 2-ого порядков. Док-во:

ХУ

a₀ s ⁿ + a₁ s ⁿ-1 + ... + a_n-1 s + a_n = 0 ,

представим в виде:

a₀ (s - s₁) (s - s₂) ... (s - s_n-1) (s - s_n) = 0 ,

где: s₁, s₂, ... s_n-1, s_n - корни.

В устойчивой системе вещественные части корней отрицательны. Подставим такие корни: s₁ = -a₁; s₂ = -a₂; s₃₄ = -a₃±jb ... :

a₀(s+a₁)(s+a₂)(s+a₃-jb)(s+a₃+jb) ... = a₀(s+a₁)(s+a₂)((s+a₃)²+b²) ... = 0

Если раскрыть скобки и вернутся к стандартному виду ХУ, то все коэффициенты уравнения получатся положительными.

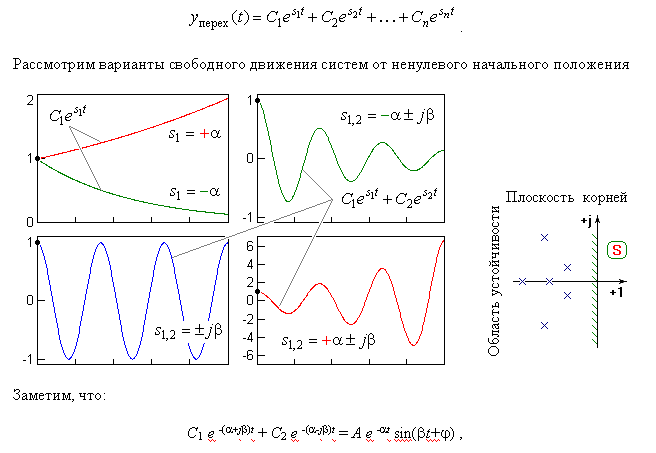
Заметим, что:

C₁ e ^-(a+jb)t + C₂ e ^-(a-jb)t = A e ^-at sin(bt+j) ,

где: A и j - новые постоянные интегрирования, a - показатель затухания, b - круговая частота затухающих колебаний.

Таким образом, для затухания переходного процесса и устойчивости линейной системы необходимо и достаточно, чтобы вещественные части корней были отрицательными, те лежали слева от мнимой оси плоскости корней.

Система будет находиться на границе устойчивости при наличии: