Дифференциальное уравнение звена: T² d²y(t)/dt² + 2rT dy(t)/dt + y(t) = k u(t), r- декремент затухания.

Передаточная функция:  W(p) = k/(T²p² + 2r Tp + 1).

Корни характеристического уравнения: p_1,2 = (-r ±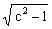)/T.

Звено будет колебательным, если корни комплексные.

Аналитическая формула переходной характеристики звена:

H(t) = k[1-exp(-gt) (cos lt+(g/l) sin lt)] 1(t), g= (l/p) ln (A₁/A₂), l= w₀.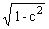

Импульсная функция: h(t) = (kw₀²/l) exp(-gt) sin(lt) 1(t).

По характеристикам реального устройства можно оценить его параметры. Постоянная времени Т и коэффициент затухания: T = T_k/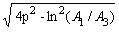,   r = ln(A₁/A₃) /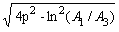, где T_k – период колебаний, А₁ и А₃ – амплитуды двух соседних полуколебаний одного знака относительно установившегося значения.

ЛАЧХ колебательного звена: L(w) = 20 lg k – 10 lg((1-T² w²)² + 4r²T²w²).