|
Интегрирующее (астатическое) звено.
Идеальное интегрирующее звено описывается дифференциальным уравнением: dy/dt = k u(t).
Общее решение: y(t) = y(0) +  k u(t) dt. Передаточная функция звена: W(p) = k/p. Переходная характеристика при u(t) = 1(t) и нулевых начальных условиях:
H(t) = k t(t) = k  1(t) dt. H(p) = k/p 2. Весовая функция при u(t) = d(t) и нулевых начальных условиях: h(t) = k 1(t). h(p) = k/p.
АФЧХ интегратора: W(jw) = k/jw = -jk/w = k exp(-jp/2)/w.
ЛАЧХ интегратора: L(w) = 20 lg |W(jw| = 20 lg k – 20 lg w.
Интегрирующее звено с замедлением.
Дифференциальное уравнение звена: T d2y(t)/dt2 + dy(t)/dt = k u(t).
Передаточная функция звена: W(p) = k/[p(Tp+1)].
Переходная характеристика: H(t) = k[t-T(1-exp(-t/T))] 1(t).
Весовая функция: h(t) = k[1-exp(-t/T)] 1(t).
Частотные характеристики звена: L(w) = 20 lg [k/( 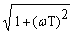 )].
|