|
Дифференциальное уравнение звена: T2 d2y(t)/dt2 + 2rT dy(t)/dt + y(t) = k u(t), r- декремент затухания.
Передаточная функция: W(p) = k/(T2p2 + 2r Tp + 1).
Корни характеристического уравнения: p 1,2 = (-r ± 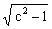 )/T. Звено будет апериодическим, если корни вещественные, или колебательным, если корни комплексные.
Если r ≥ 1, то знаменатель W(p) имеет два вещественных корня и может быть разложен на два сомножителя: T 2p 2+2rTp+1 = (T 1p+1)(T 2p+1), T 1,2 = T(r ± 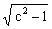 ). Переходная характеристика: H(t) = k(1-(T1/(T1-T2)) exp(-t/T1) + (T2/(T1-T2)) exp(-t/T2)) 1(t).
Весовая функция: h(t) = (k/(T1-T2)) (exp(-t/T1) – exp(-t/T2)) 1(t).
Амплитудная частотная характеристика: A(w) = k/[ 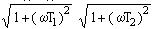 ]. Фазовая характеристика: j(w) = - argtg wT1 – argtg wT2.
|